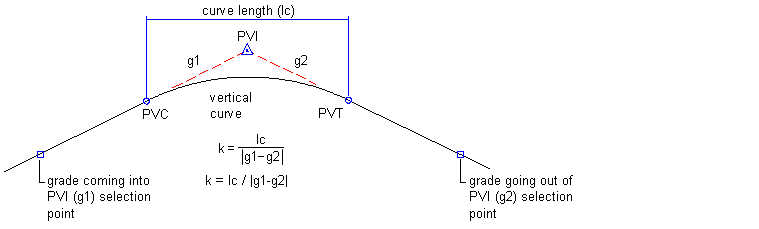
Vertical Curve K Value Formula

High or low points on a curve wh i ht di t l i dwhy.

Vertical curve k value formula. G 1 is the slope percent of the. X g 1 l g 1 g 2 g 1 r where. K rate of vertical curvature. Speed tables or other design tools often provide a target minimum k value.

The formulas below are used in the design of vertical curves. Remember you never can have a negative algebraic difference. This value represents the horizontal distance along which a 1 change in grade occurs on the vertical curve. At the highest or lowest point the tangent is horizontalat the highest or lowest point the tangent is horizontal the derivative of y w r t x 0.

Desirable k value for a crest vertical curve is 405 for english units or 120 for metric units. L k a 405 5 2025 feet or l 120 5 600 meters. Two vertical curves in the same direction separated by a short. It expresses the abruptness of the grade change in a single value.

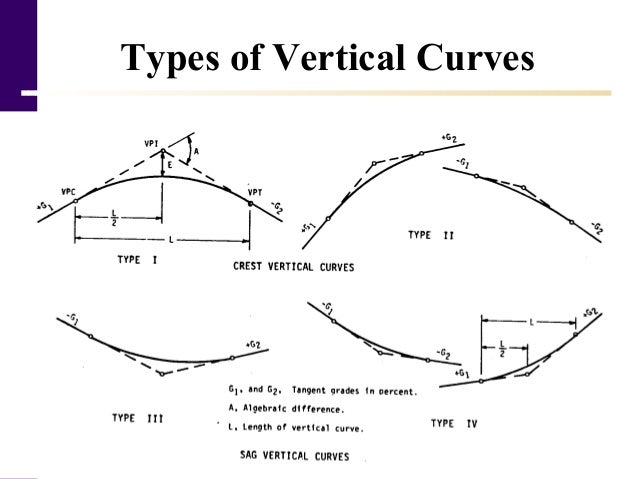
Derivinggg g the general formula gives. Are in percent. Minimum length of a crest vertical curve is equal 3 time the design speed only for english unit. Vertical curves are the second of the two important transition elements in geometric design for highways the first being horizontal curves a vertical curve provides a transition between two sloped roadways allowing a vehicle to negotiate the elevation rate change at a gradual rate rather than a sharp cut.

L total length of vertical curve. Table 6 1 contains the k values for each combination of road type design speed sight distance. Sight distance on vertical curves 6d 5 design manual chapter 6. K value in a vertical curve fyi everyone example g1 1 g2 3 so the algebraic difference 4 the formula is also correct.

In figure below vertical curve terminology is introduced. Introduce vertical curves into the alignment only when the net change in slope direction exceeds a specific value e g 1 5 percent or 2 percent. The k value is effectively an expression for degree of curvature multiplying k by 100 gives the equivalent radius of the vertical curve. Knowing k anda it is a simple matter to calculate l see next section.

Curve lengths based upon a minimum k value for small values of algebraic differences in grade a. Now solve for l the desirable length of the curve. The roller coaster or the hidden up type of profile should be avoided.